Question

Assume the random variable x is normally distributed with mean u = 90 and standard deviation o=5. Find the indicated probability.

P(X<80) =
(Round to four decimal places as needed.)

Answer 1

Given:

Let the random variable x is normally distributed with mean
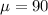`\mu=90` and
`\sigma=5`

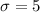
We need to determine the probability of
`P(X<80)`

Probability of
`P(X<80)`:

The formula to determine the value of
`P(X<80)` is given by

`Z=(X-\mu)/(\sigma)`

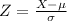
Thus, we have;

`P(X<80)=P(Z<(80-90)/(5))`

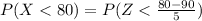
Simplifying, we get;

`P(X<80)=P(Z<(-10)/(5))`

`P(X<80)=P(Z<-2)`

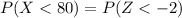
Using the normal distribution table, the value of -2 is given by 0.0228

`P(X<80)=0.0228`

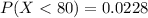
Thus, the value of
`P(X<80)` is 0.0228