Question

You are given a rectangular sheet of cardboard that measures 11 in. by 8.5 in. (see the diagram below). A small square of the same size is cut from each corner, and each side folded up along the cuts to from a box with no lid.

1. Anya thinks the cut should be 1.5 inches to create the greatest volume, while Terrence thinks it should be 3 inches.

Explain how both students can determine the formula for the volume of the box.
Determine which student's suggestion would create the larger volume.
Explain how there can be two different volumes when each student starts with the same size cardboard.
2. Why is the value of x limited to 0 in. < x < 4.25 in.?

Answer 1

Part 1) Anya's box will have larger volume as compared to Terence's box

Part 2) see the explanation

Part 3) see the explanation

Explanation:

The picture of the question in the attached figure

Part 1) Explain how both students can determine the formula for the volume of the box.

Determine which student's suggestion would create the larger volume

we know that

The volume of the box is given by the formula

`V=LWH`

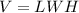
we have

`L=(11-2x)\ in\\W=(8.5-2x)\ in\\H=x\ in`

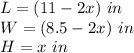
Anya

we have

x=1.5 in

so

`L=(11-2(1.5))=8\ in\\W=(8.5-2(1.5))=5.5\ in\\H=1.5\ in`

substitute in the formula of volume

`V=(8)(5.5)(1.5)=66\ in^3`

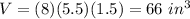
Terrence

we have

x=3 in

so

`L=(11-2(3))=5\ in\\W=(8.5-2(3))=2.5\ in\\H=3\ in`

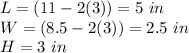
substitute in the formula of volume

`V=(5)(2.5)(3)=37.5\ in^3`

Hence,

Anya's box will have larger volume as compared to Terence's box

Part 2) Explain how there can be two different volumes when each student starts with the same size cardboard

The box's size depends on the length/width/height of the cardboard being cut, which is why different measurements / cutting methods for the same size cardboard can result in different box sizes.

Part 3) Why is the value of x limited to 0 in. < x < 4.25 in.?

The square would be cut from all four corners, therefore the sum of the 2 length sides of the squares on the cardboard cannot exceed the short side of the cardboard. The shorter side of the cardboard is 8.5 inches, divided by 2 = 4.25 inches, hence the length side of the squares cannot be larger than 4.25 inches