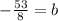Slope-intercept form: y = mx + b
(m is the slope, b is the y-intercept or the y value when x = 0 --> (0, y) or the point where the line crosses through the y-axis)
For lines to be perpendicular, their slopes have to be negative reciprocals of each other (flip the sign +/- and the fraction/switch the numerator and the denominator)
For example:
Slope = -2 or
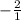
Perpendicular line's slope:
 (flip the sign from - to +, and flip the fraction)
(flip the sign from - to +, and flip the fraction)
Slope =

Perpendicular line's slope =
 or -3 (flip the sign from + to -, flip fraction)
or -3 (flip the sign from + to -, flip fraction)
y = 8x - 2 The slope is 8, so the perpendicular line's slope is
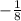 .
.
Now that you know the slope, substitute/plug it into the equation:
y = mx + b
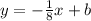 To find b, plug in the point (-5, -6) into the equation, then isolate/get the variable "b" by itself
To find b, plug in the point (-5, -6) into the equation, then isolate/get the variable "b" by itself
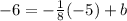 (Two negative signs cancel each other out and become positive)
(Two negative signs cancel each other out and become positive)
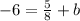 Subtract 5/8 on both sides to get "b" by itself
Subtract 5/8 on both sides to get "b" by itself
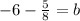 (To combine fractions, they need to have the same denominator, so multiply -6 by 8/8 so that they will have the same denominator)
(To combine fractions, they need to have the same denominator, so multiply -6 by 8/8 so that they will have the same denominator)
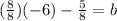
 = b Now combine the fractions
= b Now combine the fractions