Question

If prism A and prism B have a ratio of similarity of 1:4, what is the volume of prism B if the

volume of prism A is 83 cubic units?

Answer 1

Volume of Prism B: 5312 units^3

Explanation:

• we know that the ratio of prism A and prism B is 1:4
• 1:4 is the same as 1/4

• to find the volume ratio of similarity of the new figure you have to cube the ratio: 1/4^3 = 1/64
• now that we know what the volume ratio is, we can now set up a table:

1/64=83/x (x is B and 83 is A)

Cross multiply: 1·x

64·83

• now we have an equation: 1x=5312
• answer: V= 5312 units cubed

Answer 2

Prism B = 332 Cubic Units

Explanation:

"prism A and prism B have a ratio of similarity of 1:4"

1:4 is the same as
`(1)/(4)` or
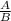`(A)/(B)` this just means that A is 25% of B because 1/4=.25

that means that for A to = B you have to multiply A x 4

so A=83 we plug it into the equation and we get 83 x 4 = 332

A : B = 83 : 332