Question

Suppose a baseball pitcher throws the ball to his catcher.

a. Is the change in speed of the ball different when the pitcher is throwing the ball compared to the catcher receiving the ball? Or is it the same?
b. Is the change in momentum greater for the pitcher or the catcher? Or is it the same either way?
c. In which case is the impulse greater? Or is it the same?
d. Does it take longer to throw the ball or catch it?
e. Does it take more force to throw the ball or catch it?

Answer 1

The change in speed of the baseball differs when thrown by the pitcher and caught by the catcher, whereas the change in momentum and impulse are the same for both. The force to throw the ball can be considered greater than to catch it.

Step-by-step explanation:

When comparing the processes of a baseball pitcher throwing a ball and a catcher receiving it, we can address each part of the question as follows:

• a. The change in speed of the ball is different for the pitcher and the catcher. The pitcher accelerates the ball from rest to a certain speed, while the catcher decelerates the ball to rest.
• b. The change in momentum is the same for both the pitcher and the catcher because momentum change is dependent on the mass and velocity change of the ball, which are consistent whether it is being thrown or caught.
• c. The impulse is also the same for both the pitcher and the catcher, as the impulse is the product of force and the time over which the force is applied, which corresponds to the change in momentum.
• d. The time it takes to throw or catch the ball can vary based on technique, but in theory, either action can be completed in similar time frames.
• e. The force required to throw the ball is generally greater than to catch it since the pitcher must generate the speed of the ball from rest, whereas the catcher is only stopping the ball's motion.

Answer 2

a) Same

b) Same

c) Same

d) Throw the ball takes longer

e) F is larger when the ball is catched

Step-by-step explanation:

a)

The change in speed of an object is given by:

`\Delta v = |v-u|`

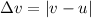
where

u is the initial velocity of the object

v is the final velocity of the object

The change in speed is basically the magnitude of the change in velocity (because velocity is a vector, while speed is a scalar, so it has no direction).

In this problem:

- In situation 1 (pitcher throwing the ball), the initial velocity is

u = 0 (because the ball starts from rest)

while the final velocity is v, so the change in speed is

`\Delta v=|v-0|=|v|`

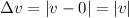
- In situation 2 (catcher receiving the ball), the initial velocity is now

u = v

while the final velocity is now zero (ball coming to rest), so the change in speed is

`\Delta v =|0-v|=|-v|`

Which means that the two situations have same change in speed.

b)

The change in momentum of an object is given by

`\Delta p = m \Delta v`

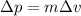
where

m is the mass of the object

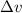`\Delta v` is the change in velocity

If we want to compare only the magnitude of the change in momentum of the object, then it is given by

`|\Delta p|=m|\Delta v|`

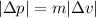
- In situation 1 (pitcher throwing the ball), the change in momentum is

`\Delta p = m|\Delta v|=m|v|=mv`

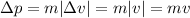
- In situation 2 (catcher receiving the ball), the change in momentum is

`\Delta p = m\Delta v = m|-v|=mv`

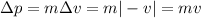
So, the magnitude of the change in momentum is the same (but the direction is opposite)

c)

The impulse exerted on an object is equal to the change in momentum of the object:

`I=\Delta p`

where

I is the impulse

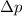`\Delta p` is the change in momentum

As we saw in part b), the change in momentum of the ball in the two situations is the same, therefore the impulse exerted on the ball will also be the same, in magnitude.

However, the direction will be opposite, as the change in momentum has opposite direction in the two situations.

d)

To compare the time of impact in the two situations, we have to look closer into them.

- When the ball is thrown, the hand "moves together" with the ball, from back to ahead in order to give it the necessary push. We can verify therefore that the time is longer in this case.

- When the ball is cacthed, the hand remains more or less "at rest", it doesn't move much, so the collision lasts much less than the previous situation.

Therefore, we can say that the time of impact is longer when the ball is thrown, compared to when it is catched.

e)

The impulse exerted on an object can also be rewritten as the product between the force applied on the object and the time of impact:

`I=F\Delta t`

where

I is the impulse

F is the force applied

`\Delta t` is the time of impact

This can be rewritten as

`F=(I)/(\Delta t)`

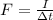
In this problem, in the two situations,

- I (the impulse) is the same in both situations

-
`\Delta t` when the ball is thrown is larger than when it is catched

Therefore, since F is inversely proportional to
`\Delta t`, this means that the force is larger when the ball is catched.