Given:
The height of the bird at time t is given by the function
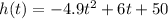
We need to determine the time it takes the worm to be eaten by the bird.
Time taken:
The time can be determined by substituting h(t) = 0 in the function.
Thus, we have;
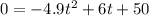
Switch sides, we get;
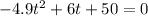
Let us solve the equation using the quadratic formula.
Thus, we get;
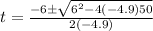
Simplifying, we get;
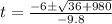
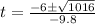
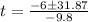
The values of t are given by
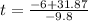 and
and

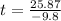 and
and
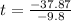
 and
and

Since, the value of t cannot be negative, then

Thus, the time taken by the bird to eat the worm is
 seconds.
seconds.
Hence, Option B is the correct answer.