Question

Which equation does this image represent?

Answer 1

Given:

Image of the ellipse

To find:

The equation of the image

Solution:

The given image is a ellipse.

Center of the ellipse = (0, 0)

x-axis points are (-3, 0) and (3, 0).

y-axis points are (2, 0) and (-2, 0).

Standard form of equation of ellipse:

`$((x-h)^(2))/(a^(2))+((y-k)^(2))/(b^(2))=1`

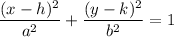
where (h, k) is the center = (0,0)

a is the point on x-axis where y = 0. Hence a = 3.

b is the point on y-axis where x = 0. Hence b = 2.

Substitute this in the standard form of ellipse.

`$((x-0)^(2))/(3^(2))+((y-0)^(2))/(2^(2))=1`

`$(x^(2))/(9)+(y^(2))/(4)=1`

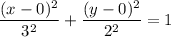
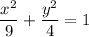
To make the denominator same multiply 1st term by
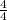`(4)/(4)` and 2nd term by
`(9)/(9)`.

`$(4x^(2))/(4*9)+(9y^(2))/(9*4)=1`

`$(4x^(2))/(36)+(9y^(2))/(36)=1`

`$(4x^(2)+9y^(2))/(36)=1`

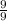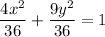
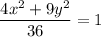
Multiply by 36 on both sides

`$(4x^(2)+9y^(2))/(36)* 36=1* 36`

`${4x^(2)+9y^(2)}={36}`

The equation of the image is
`${4x^(2)+9y^(2)}={36}`.