Given:
The given expression is
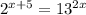
We need to determine the value of x using either base - 10 or base - e logarithms.
Value of x:
Let us determine the value of x using the base - e logarithms.
Applying the log rule that if
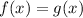 then
then
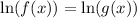
Thus, we get;

Applying the log rule,
 , we get;
, we get;
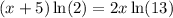
Expanding, we get;
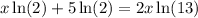
Subtracting both sides by
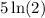 , we get;
, we get;
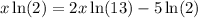
Subtracting both sides by
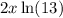 , we get;
, we get;
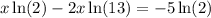
Taking out the common term x, we have;

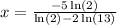

Thus, the value of x is
