Answer:
The points that are the approximate locations of the foci of the ellipse are (0,√13) and (0,-√13) or, what is the same, (0,3.60) and (0,-3.60)
Explanation:
The equation
 follows the following form of representation of an ellipse:
follows the following form of representation of an ellipse:
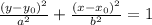
where x₀ and y₀ are the values of x and y in the center of the ellipce and a nab b are the values of the major and minor semiaxis, respectively. So the major axis is vertical in this case.
Being c the focal length, the relationship between the focal length and the semi-axes is:
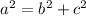 The foci are located on the major axis
The foci are located on the major axis
In this case: 49=36+c²
Solving: c²=49-36
c²=13
c=√13 ≅ 3.60
So, the points that are the approximate locations of the foci of the ellipse are (0,√13) and (0,-√13) or, what is the same, (0,3.60) and (0,-3.60)