Question

For a sample of nequals37​, find the probability of a sample mean being less than 12 comma 749 or greater than 12 comma 752 when muequals12 comma 749 and sigmaequals1.5.

Answer 1

0.500 is the required probability.

Explanation:

We are given the following information in the question:

Mean, μ = 12,749

Standard Deviation, σ = 1.5

Let X be the distribution of sample means.

Formula:

`z_(score) = \displaystyle(x-\mu)/(\sigma)`

Standard error due to sampling =

`=(\sigma)/(√(n)) = (1.5)/(√(37)) = 0.2465`

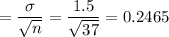
We have to evaluate:

P(x less than 12,749 or greater than 12,752)

`= 1 - P(12749\leq x \leq 12752)`

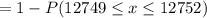
Now,

`P(12749\leq x \leq 12752)\\\\ = P(\displaystyle(12749 - 12749)/(0.2465) \leq z \leq \displaystyle(12752-12749)/(0.2465)) \\\\= P(0 \leq z \leq 12.17)\\\\= P(z \leq 12.17) - P(z < 0)\\= 1.000 - 0.500 = 0.500`

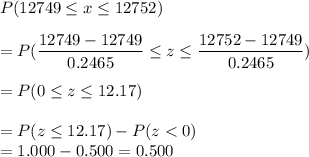
P(x less than 12,749 or greater than 12,752)

`= 1 - P(12749\leq x \leq 12752)\\=1-0.500\\=0.500`

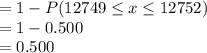
Thus, 0.500 is the required probability.