Question

In a large bag of marblesb20% of them are red.A child chooses 4 marbles.If the child chooses the marbles at random what is the chance of getting three exact red marble

Answer 1

The probability if 3 marbles being red and 1 non red

=
`(0.2 m) * ((0.2 m - 1)/(m-1)) * ((0.2 m - 2)/(m-2)) * ((0.8 m )/(m-3))`

Explanation:

Here, let us assume that the total number of the marbles in the bag = m

Now, as given :

The total percentage of red marbles in bag = 20% of m

So, total red marbles = 0.2 m

Marbles which are not red = m - 0.2 m = 0.8 m

The number of marbles chosen at random = 4

Now, probability of getting first red marble =
`\frac{\textrm{Total Red Marbles}}{\textrm{Total Marbles }} = (0.2 m)/(m) = 0.2`

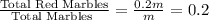
Again, total marbles left = m - 1

Probability of getting second red marble =
`\frac{\textrm{Total Red Marbles}}{\textrm{Total Marbles }} = (0.2 m - 1 )/(m-1)`

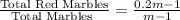
Again, total marbles left = m - 2

Probability of getting third red marble =
`\frac{\textrm{Total Red Marbles}}{\textrm{Total Marbles }} = (0.2 m - 2 )/(m-2)`

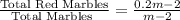
Again, total marbles left = m - 3

Probability of getting fourth non - red marble =
`\frac{\textrm{Total non Red Marbles}}{\textrm{Total Marbles }} = ((0.8 m )/(m-3))`

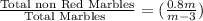
So, the probability if 3 marbles being red and 1 non red

=
`(0.2 m) * ((0.2 m - 1)/(m-1)) * ((0.2 m - 2)/(m-2)) * ((0.8 m )/(m-3))`