Question

Write the standard equation of a circle that passes through (−2, 10) with center (−2, 6).

A: (x + 2)2 + (y – 10)2 = 8

B: (x + 2)2 + (y – 6)2 = 16

C: (x + 2)2 + (y – 6)2 = 4

D: (x – 2)2 + (y + 10)2 = 16

Answer 1

The answer you’re looking for is B

Answer 2

The answer to your question is the letter B.

Explanation:

Data

Point = (-2, 10)

Center = (-2, 6)

Process

1.- Find the radius using the distance between two points

dCP =
`\sqrt{(x2 - x1)^(2)+ (y2 - y1)^(2)}`

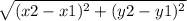
-Substitution

dCP =
`\sqrt{(-2 + 2)^(2)+ (6 - 10)^(2)}`

dCP =
`\sqrt{(0)^(2)+ (-4)^(2)}`

dCP =
`√(16)`

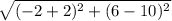
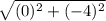
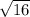
dCP = 4

2.- Write the equation of the circle

Standard equation (x - h)² + (y - k)² = r²

h = -2

k = 6

r = 4

(x + 2)² + (y - 6)² = 4²

Equation (x + 2)² + (y - 6)² = 16