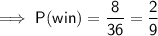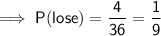Answer:
**Please see attached for the sample space**
- The winning combinations are highlighted in green.
- The losing combinations are highlighted in red.
From inspection of the sample space:
- Total number of ways the sum is 7 or 11 (win) = 8
- Total number of ways the sum is 2, 3 or 12 (lose) = 4
- Total number of possible outcomes = 36