Question

Rob invests $3,715 in a retirement account

with a fixed annual interest rate of 9%
compounded 3 times per year. What will
the account balance be after 15 years?

Answer 1

$14,048.62

Explanation:

The interest is 9% per year and compounded 3 times a year, so each compound will be 9%/3 = 3%

The time elapsed will be 15 years and the interest compounded 3 times a year, so the number of compounds happens will be = 15 years* 3 compounds/year= 45x compound.

So basically the money will get 3% interest 45 times. To put into the compounding interest formula, the final account balance will be:

A = P (1 + [ r / n ]) ^ nt

A= amount of the balance after a period of t

P= principal, the initial money deposit( $3,715)

r= rate(9%)

n= number of compound per unit of time(3 times per year)

t= time(15 years)

The calculation will be:

A = P (1 + [ r / n ]) ^ nt

A =
`$3,715((1+0.09)/(3) )^(3*15)`

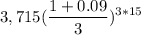
A = $14,048.62