Question

Two persons A and B are on the same side of a tower (T). Ifthe angles of elevation of the top of the tower as observed by A and B are 40°and 55° respectively and line /AB/ is 6m. Find the height of the tower.

Answer 1

12.2 meters

Explanation:

The position of tower and the two persons has been shown in the figure below.

Let, h is the height of tower and the distance between tower and person B is x.

We can see in the figure that there are two triangles PAQ and PBQ and both are right angle triangles.

Now, In triangle PAQ, we can write

tan40⁰ =
`(h)/(x+6)`

Thus, 0.839 =
`(h)/(x+6)`

`0.839x + 5.034 = h`

`x = (h- 5.034)/(0.839)` (equation 1)

Again, in triangle PBQ, we can write

tan55⁰ =
`(h)/(x)`

Thus, 1.428 =
`(h)/(x)`

`x = (h)/(1.428)` (equation 2)

Now, from equation 1 and equation 2, we can write

`(h-5.034)/(0.839) = (h)/(1.428)`

`1.428h - 7.188 = 0.839h`

`0.589h=7.188`

`h=12.2`

Thus the height of the tower will be 12.2 meters.

Answer 2

Height of the tower is 12.07 meter.

Explanation:

Given:

Angle of elevation observed from A = 40°

Angle of elevation from point B = 55°

Distance from A to B = 6 m

Note :

As we move towards the tower the angle of elevation will increase.

Let the height of the tower be "h'' meter.

And the distance from B to the base of the tower be "x'' m.

Adjacent length for angle 55° is ''x'' m and adjacent length from point A that is angle 40° is "6+x" m.

And we know that:

⇒
`tan (\theta) = (opposite)/(adjacent)`

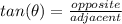
So arranging them in tangent angles.

⇒
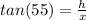`tan(55) = (h)/(x)` ...equation (i)

⇒
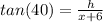`tan(40)=(h)/(x+6)` ...equation (ii)

Dividing both the equation.

⇒
`(tan(55))/(tan(40)) =(h)/(x)* (6+x)/(h)`

⇒
`1.7=(6+x)/(x)`

⇒
`1.7x=6+x`

⇒
`1.7x-x=6`

⇒
`0.7x=6`

⇒
`x=(6)/(0.7)`

⇒
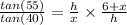
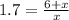
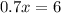
`x=8.5` m

Now using the value of 'x' in equation (i).

⇒
`h=x* tan(55)`

⇒
`h=8.5(1.42)`

⇒
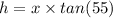
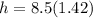
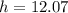`h=12.07` m

Height of the tower is 12.07 meter.