Answer:
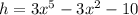
Explanation:
We have been given that volume of a certain cylinder is
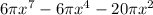 and base area is
and base area is
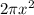 . We are asked to find the height of the cylinder.
. We are asked to find the height of the cylinder.
We know that a cylinder's volume can be calculated by the formula
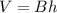 , where V stands for volume, B stands for base area, and h stands for height.
, where V stands for volume, B stands for base area, and h stands for height.
Let us solve for h.
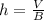
Upon substituting our given values, we will get:
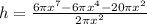
Let us factor out
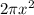 from numerator.
from numerator.
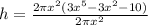
Upon cancelling out same terms, we will get:
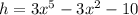
Therefore, the height of the cylinder would be
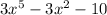 units.
units.