Question

NASA is conducting an experiment to find out the fraction of people who black out at G forces greater than 6 6 . In an earlier study, the population proportion was estimated to be 0.32 0.32 . How large a sample would be required in order to estimate the fraction of people who black out at 6 6 or more Gs at the 85% 85 % confidence level with an error of at most 0.03 0.03 ? Round your answer up to the next integer.

Answer 1

The sample size must be atleast 502 to have a margin of error of 0.03

Explanation:

We are given the following in the question:

Proportion = 0.32

`\hat{p} = 0.32`

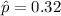
Level of significance = 0.15

Margin of error = 0.03

Formula for margin of error =

`z_(stat)* \sqrt{\frac{\hat{p}(1-\hat{p})}{n}}`

`z_(critical)\text{ at}~\alpha_(0.15) = 1.44`

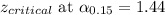
We have to find the sample size such that the margin of error is atmost 0.03.

Putting values, we get,

`z_(stat)* \sqrt{\frac{\hat{p}(1-\hat{p})}{n}}\leq 0.03\\\\1.44* \sqrt{(0.32(1-0.32))/(n)}\leq 0.03\\\\√(n)\geq 1.44* (√(0.32(1-0.32)))/(0.03)\\\\√(n)\geq 22.39\\n\geq 501.3121\\\Rightarrow n\geq 502`

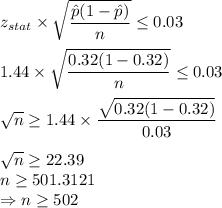
Thus, the sample size must be atleast 502 to have a margin of error of 0.03 in approximation of proportion of people who would black out at 6 or more Gs.