Answer:
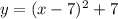 .
.
Explanation:
Let
 ,
,
 , and
, and
 be constants, and let
be constants, and let
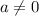 . The equation
. The equation
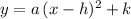 represents a parabola in a plane with vertex at
represents a parabola in a plane with vertex at
 .
.
For example, for
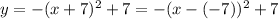 ,
,
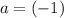 ,
,
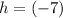 , and
, and
 .
.
A parabola is entirely above the
 -axis only if this parabola opens upwards, with the vertex
-axis only if this parabola opens upwards, with the vertex
 above the
above the
 -axis.
-axis.
The parabola opens upwards if and only if the leading coefficient is positive:
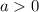 .
.
For the vertex
 to be above the
to be above the
 -axis, the
-axis, the
 -coordinate of that point,
-coordinate of that point,
 , must be strictly positive. Thus,
, must be strictly positive. Thus,
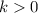 .
.
Among the choices:
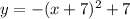 does not meet the requirements. Since
does not meet the requirements. Since
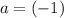 , this parabola would open downwards, not upwards as required.
, this parabola would open downwards, not upwards as required.
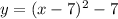 does not meet the requirements. Since
does not meet the requirements. Since
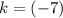 and is negative, the vertex of this parabola would be below the
and is negative, the vertex of this parabola would be below the
 -axis.
-axis.
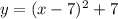 meet both requirements:
meet both requirements:
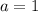 and
and
 .
.
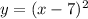 (for which
(for which
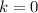 ) would touch the
) would touch the
 -axis at its vertex.
-axis at its vertex.