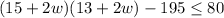Question

a rectangle garden measuring 13 meters by 15meters is to have agravek pathway of constant width built all around it. there is wnough gravel to cover 80 sqaure meters or less. enter an inequality that represents all the posible width, in meters, of the pathway

Answer 1

Answer:
`(15+2w)(13+2w)-195\leq 80`

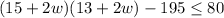
Explanation:

The area of a rectangle can be calculated multiplying its dimensions.

Observe the figure attached, where "w" is the constant width of the gravel pathway around the rectangular garden.

You can notice that the length of the rectangular garden is 15 meters and the width is 13 meters. Then, its area is:

`A_g=(15\ m)(13\ m)\\\\A_g=195\ m^2`

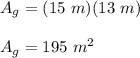
Based on the figure, you can determine that the dimensions of the pathway around the garden are:

`length=(15+2w)\\\\width=(13+2w)`

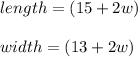
Therefore, the area of that gravel pathway would be:

`(15+2w)(13+2w)-195=A_p`

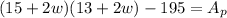
Its area must be less than or equal to 80 square meters, then you can write the following inequality that represents all the posible width, in meters, of the pathway:

`(15+2w)(13+2w)-195\leq 80`