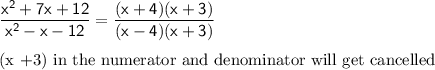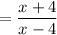Answer:
Explanation:
Factorize the expression.
Sum = 7
Product = 12
Factors = 4 , 3
4 + 3= 7 & 4*3 = 12
x² + 7x + 12 = x² + 4x + 3x + 4*3
= x(x + 4) + 3(x + 4)
= (x + 4)(x + 3)
Sum = -1
Product = -12
Factors = (-4) , 3
(-4) + 3 = (-1) & (-4)*3 = -12
x² - x - 12 = x² - 4x + 3x - 4*3
= x(x - 4) +3(x - 4)
= (x -4)(x +3)