Given:
The coordinates of the triangle RST are (0,1), (-2,2) and (-1,4)
The coordinates of the triangle R'S'T' are (1,0), (2,2) and (4,1)
We need to determine the rotation about origin.
Rotation about the origin:
To determine the rotation about the origin, we need to find the translation rule.
The coordinates of the point R to R' is
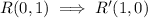
The translation rule for the point R to R' is

The coordinate of the point S to S'is

The translation rule for the point S to S' is

The coordinates of the point T to T' is
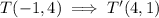
The translation rule for the point T to T' is

Therefore the rule to translate the triangle RST to R'S'T' is

Hence, the triangle is rotated 90° clockwise about the origin.
Hence, Option a is the correct answer.