Question

How do you express the interval in set builder notation station and graph the interval on the number line ( 2, 8]

Answer 1

The graph is below in the attached image.

The answer in set builder notation is
`\{x | x \in \mathbb{R}, \ 2 < x \le 8\}`

The interval notation (2, 8] means the interval starts at 2 and ends at 8. The curved parenthesis tells us to exclude 2 from the interval. This is visually represented as an open hole on the graph. In contrast, 8 is included due to the square bracket. A closed filled in hole is used to show this. Everything between the endpoints is shaded in as the blue region on the graph.

Since we exclude 2, but include 8, we can say that (2, 8] turns into
`2 < x \le 8`

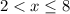
Then we surround that with curly braces adding on the portion
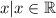`x | x \in \mathbb{R}` which says "x such that x is a real number"

All together we end up with this set builder notation
`\{x | x \in \mathbb{R}, \ 2 < x \le 8\}` and it means "the set of all real numbers x such that x is between 2 and 8, excluding 2 but including 8"