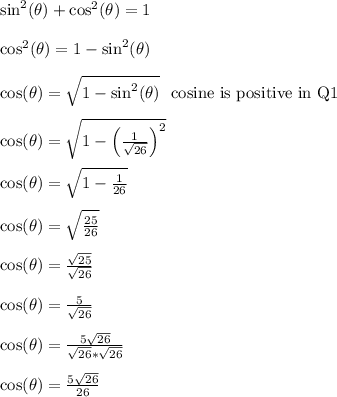Answer:
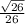
This is the square root of 26 over 26. The second 26 is not inside the square root. You can type it in as sqrt(26)/26.
========================================================
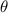 is in Q1 so
is in Q1 so
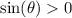
Use the trig identity below and plug in the given value to get...
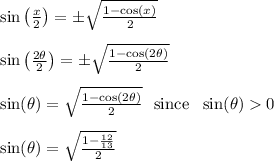

------------------------------
Edit:
To find cos(theta), we use the pythagorean identity below