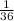Question

A red die and a blue die are tossed.

Determine the probability of the red die showing a 3 and the blue die showing a 3.
Express your answer as a simplified fraction.

Answer 1

`P(3,red \ and\ 3, blue)=(1)/(36)`

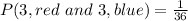
Explanation:

-A fair die has 6 faces, a sample space of 6 and each space has a probability of 1/6:

#The probability of 3 in the red die;

`P(3,red)=(1)/(6)`

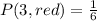
#The probability of 3 in blue die:

`P(3,blue)=(1)/(6)`

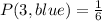
The probability of a 3 in both dice is the product of the individual probabilities:

`P(3,red and 3, blue)=P(3,red)* P(3,blue)\\\\=(1)/(6)* (1)/(6)\\\\=(1)/(36)`

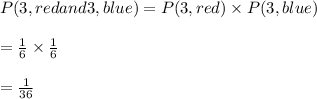
Hence, the probability of a 3 in both dice is
`(1)/(36)`