Question

Find the sum of 14 + 8 + 2+ ... + ( 274) + (-280).

Answer 1

The sum of the given sequence is -6384.

Explanation:

The given Arithmetic sequence is 14 + 8 + 2+ ... + ( 274) + (-280).

• The first term of the sequence = 14
• The last term of the sequence = -280
• The common difference ⇒ 14 - 8 = 6

To find the number of terms in the sequence :

The formula used is
`n = (\frac{a_(n)-a_(1)} {d})+1`

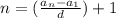
where,

• n is the number of terms.
• 
  `a_(n)` is the late term which is -280.
• 
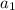  `a_(1)` is the first term which is 14.
• d is the common difference which is 6.

Therefore,
`n =((-280-14)/(6)) +1`

⇒
`n =( (-294)/(6)) + 1`

⇒
`n = -49 + 1`

⇒
`n = -48`

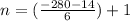
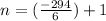
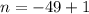
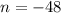
⇒ n = 48, since n cannot be negative.

∴ The number of terms, n = 48.

To find the sum of the arithmetic progression :

The formula used is
`S = (n)/(2)(a_(1) + a_(n) )`

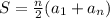
where,

• S is the sum of the sequence.
• 
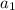  `a_(1)` is the first term which is 14.
• 
  `a_(n)` is the late term which is -280.

Therefore,
`S = (48)/(2)(14+ (-280))`

⇒
`S = (48)/(2)(-266)`

⇒
`S = 48 * -133`

⇒
`S = -6384`

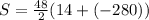
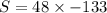
∴ The sum of the given sequence is -6384.