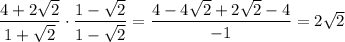Question

Find the value of x given that


`\sqrt{x + 8 \sqrt{x + 8 √( x + 8 ) } } = 2 (7)/(2)`
b)Given that x=3+2✓2,find the value of √x +1/√x​

Answer 1

For the first part, the results get quite crazy. I hardly believe that you're supposed to do this by hand, so I'm afraid that there's some typo in the question.

As for the second part, we have

`√(x)+(1)/(√(x))=(x+1)/(√(x))`

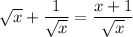
Plug your value for x and you have

`(x+1)/(√(x)) \mapsto \frac{4+2√(2)}{\sqrt{3+2√(2)}}=(4+2√(2))/(1+√(2))`

We can rewrite the quantity as

`(4+2√(2))/(1+√(2))\cdot(1-√(2))/(1-√(2))=(4-4√(2)+2√(2)-4)/(-1) = 2√(2)`