Question

A) Given: Lateral area = 156 SK = 10, Find: m∠KSM

Answer 1

m∠KSM = 59.55°

Explanation:

The formula of the lateral area of a cone is LA =
`(1)/(2)` Cl, where c is the circumference of the base and l is the slant height

The formula of the circumference of a circle is C = 2πr

From the figure

SO is the height of the cone

KM is the diameter of the base

SO⊥ KM

SK and SM are slant heights

We can use the trigonometry ratio in triangle SOK to find angle KSO, then multiply its measure by 2 to find the measure of ∠KSM, because m∠KSO is equal to m∠MSO

∵ LA =
`(1)/(2)` Cl

∵ C = 2πr

∴ LA =
`(1)/(2)` (2πr) l

∴ LA = πrl

∵ LA = 156

- l is the side SK

∵ SK = 10 units

∴ l = 10

- Substitute the values of LA and l in the formula above

∵ 156 = 10πr

- Divide both sides by 10π

∴
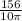`(156)/(10\pi )` = r

∴ r =
`(78)/(5\pi )`

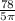
∵ sin(∠KSO) =
`(OK)/(SK)`

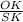
∵ OK is the radius of the base

∴ sin(∠KSO) =
`((78)/(5\pi ))/(10)`

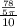
∴ sin(∠KSO) =
`(39)/(25\pi )`

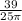
- Use
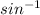`sin^(-1)` to find m∠KSO

∴ ∠KSO =
`sin^(-1)(39)/(25\pi )`

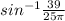
∴ ∠KSO = 29.77°

∵ m∠KSO = m∠MSO

∴ m∠KSM = 2 m∠KSO

∴ m∠KSM = 2(29.77°)

∴ m∠KSM = 59.55°