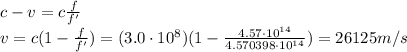Question

A hydrogen line in a star's spectrum has a frequency of 4.57x10^14 Hz when stationary. In Altair's spectrum, it is shifted upward by 3.98x10^10 Hz. What is Altair's velocity relative to us? (Unit=m/s)

Answer 1

26125 m/s

Step-by-step explanation:

The Doppler effect occurs when there is a source of a wave in relative motion with respect to an observer. In this situation, the frequency of the wave observed by the observer appears to be shifter with respect to the real frquency. In particular:

- If the source of the wave is moving away from the observer, there is an appareant decrease in frequency

- If the source of the wave is moving towards the observer, there is an apparent increase in frequency

This phenomenon occurs with any type of waves, also with light waves.

For light waves, the apparent frequency of the light emitted by the source is given by:

`f'=(c)/(c\pm v)f`

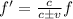
where

f' is the observed frequency

f is the real frequency

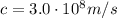`c=3.0\cdot 10^8 m/s` is the speed of light in a vacuum

`v` is the velocity of the source, which is positive if the source is moving away, negative if the source is moving towards the observer

Here we have:

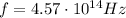`f=4.57\cdot 10^(14)Hz` is the real frequency of the hydrogen line

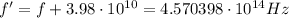`f'=f+3.98\cdot 10^(10)=4.570398\cdot 10^(14) Hz` is the observed frequency

The observed frequency is higher than the real frequency, so the star is moving towards us; so the equation will have a negative sign for the velocity:

`f'=(c)/(c-v)f`

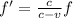
Where here v is the velocity of the star. Solving for v, we find:

`c-v=c(f)/(f')\\v=c(1-(f)/(f'))=(3.0\cdot 10^8 )(1-(4.57\cdot 10^(14))/(4.570398\cdot 10^(14)))=26125 m/s`