Question

In studies for a​ medication, 3 percent of patients gained weight as a side effect. Suppose 643 patients are randomly selected. Use the normal approximation to the binomial to approximate the probability that

​(a) exactly 24 patients will gain weight as a side effect.
​(b) 24 or fewer patients will gain weight as a side effect.
​(c) 11 or more patients will gain weight as a side effect.
​(d) between 24 and 28​, ​inclusive, will gain weight as a side effect.

Answer 1

Part a)

It was given that 3% of patients gained weight as a side effect.

This means

`p = 0.03`

`q = 1 - 0.03 = 0.97`

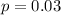
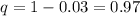
The mean is

`\mu = np`

`\mu = 643 * 0.03 = 19.29`

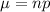
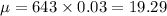
The standard deviation is

`\sigma = √(npq)`

`\sigma = √(643 * 0.03 * 0.97)`

`\sigma =4.33`

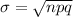
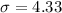
We want to find the probability that exactly 24 patients will gain weight as side effect.

P(X=24)

We apply the Continuity Correction Factor(CCF)

P(24-0.5<X<24+0.5)=P(23.5<X<24.5)

We convert to z-scores.

`P(23.5 \: < \: X \: < \: 24.5) = P( (23.5 - 19.29)/(4.33) \: < \: z \: < \: (24.5 - 19.29)/(4.33) ) \\ = P( 0.97\: < \: z \: < \: 1.20) \\ = 0.051`

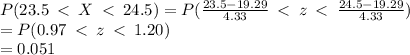
Part b) We want to find the probability that 24 or fewer patients will gain weight as a side effect.

P(X≤24)

We apply the continuity correction factor to get;

P(X<24+0.5)=P(X<24.5)

We convert to z-scores to get:

`P(X \: < \: 24.5) = P(z \: < \: (24.5 - 19.29)/(4.33) ) \\ = P(z \: < \: 1.20) \\ = 0.8849`

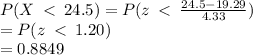
Part c)

We want to find the probability that

11 or more patients will gain weight as a side effect.

P(X≥11)

Apply correction factor to get:

P(X>11-0.5)=P(X>10.5)

We convert to z-scores:

`P(X \: > \: 10.5) = P(z \: > \: (10.5 - 19.29)/(4.33) ) \\ = P(z \: > \: - 2.03)`

`= 0.9788`

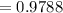
Part d)

We want to find the probability that:

between 24 and 28, inclusive, will gain weight as a side effect.

P(24≤X≤28)=

P(23.5≤X≤28.5)

Convert to z-scores:

`P(23.5 \: < \: X \: < \: 28.5) = P( (23.5 - 19.29)/(4.33) \: < \: z \: < \: (28.5 - 19.29)/(4.33) ) \\ = P( 0.97\: < \: z \: < \: 2.13) \\ = 0.1494`