Answer:
Mr. Green is the murderer.
Explanation:
Forget all the word problem bs. Just focus on the numbers.
You're given the equation

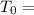 initial temp
initial temp
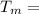 temp of room
temp of room
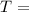 temp after t hours
temp after t hours
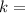 how fast the temp is changing
how fast the temp is changing
t = time (hours)
1.) We're given:
It took 1 hour for the body to go from 82.7° to 80.8° when the police found the body. The room temperature was 65°
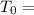 82.7°
82.7°
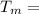 65°
65°
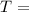 80.8°
80.8°
t = 1
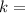 ???
???
the only thing we don't know is the value for k, so lets solve for it.
REFER TO STEP (1) in the picture.
You should get that
 . This is how fast the body was loosing heat.
. This is how fast the body was loosing heat.
2.) Now we know what k is (how fast the temperature is dropping), we can use it to find how long it took for his fresh body (98.6°) to drop to 82.7° when the police found it.
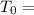 98.6°
98.6°
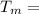 65°
65°
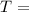 82.7°
82.7°
t = ???

We don't know what t is so lets solve for it. t will tell us how long before the police arrive (9:00pm) did the murder happened.
REFER TO STEP (2) in the picture.
You should get t=5.5079 hours. This means the murder happens 5.5 hours before 9:00pm.
3.) Since you know that the murder happened 5.5 hours before 9:00pm, subtract it.
9:00 - 5.5hours = 3:30pm
The murder happened around 3:30pm.
Mr. Green is lying because he said that he was fishing around 3:45pm-5:00pm, but that's when the murder occured.