Question

JC and D

If 990.J of heat is absorbed by a 59 g sample of water at 21.0 °C, what
will the final temperature of this sample be after absorbing this energy
The specific heat of water is 4.18 J/9g °C). *
25 degrees Celsius
O
35 degrees Celsius
o
2.5 degrees Celsius

Answer 1

25 degrees celsius will be the final temperature of this sample be after absorbing this energy

Step-by-step explanation:

data given:

q (heat absorbed) = 990 J

m (mass) = 59 gram

T2 (final temperature) = ?

c (specific heat capacity of water) = 4.18 J/g °C).

T1 (initial temperature) = 21

ΔT = T2 -T1

applying the formula for heat absorbed

q = mcΔT

putting the values in the equation

ΔT =
`(q)/(mc)`

T2 - 21 =
`(990)/(59 X4.18)`

T2 -21 = 4.01

T2 = 4.01 + 21

= 25.01 degrees

The final temperature of water sample is 25 degrees when initial temperature was 21 degrees and heat absorbed was 900 J

Answer 2

The final temperature after absorbing the energy of 990 J is 25.014 °C.

Step-by-step explanation:

The specific heat capacity formula can be used to solve the given problem.

So here the heat absorbed or the Q value is given as 990 J. Then the mass of the sample of water m is given as 59 g. The initial temperature is said to be 21 °C and the final temperature has to be determined.

The specific heat capacity is given as 4.18 J/g°C.

Then,
`Q = m*c* del T`

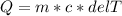
So, the difference in temperature or the change in temperature has to be determined first.

`del T = (Q)/(mc) = (990)/(59*4.18) = (990)/(246.62) \\\\del T =4.014`

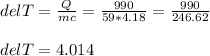
So, the change in temperature = ΔT = T₂-T₁ = 4.014 °C

T₂-21 = 4.014

T₂ = 4.014+21 = 25.014 °C.

So, the final temperature after absorbing the energy of 990 J is 25.014 °C.