Question

A string has 8 N of tension. When it is vibrated at 2 Hz, a standing wave forms with a wavelength of 4 cm and an amplitude of 1 cm. a bead of negligible mass is glued to the middle of the string.

If the bead is at a node, what total distance will it move in 1 second?

Answer 1

Total distance moved by bead is 1.952 cm.

Step-by-step explanation:

Let first consider all data that are given in question.

1. F = 8 N ...force acting on string

2. f = 2 Hz ...frequency of system

3. β = 4 cm = 0.04 m ...wavelength of wave formed due to vibration

4. A = 1 cm = 0.01 m ...Amplitude of vibration

Under certain conditions, waves can bounce back and forth through a particular region, effectively becoming stationary. These are called standing waves.

Here,it is due to vibration induced in spring due to tension induced in string

Standing wave equation is given by

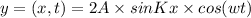`y=(x,t)= 2A * sin Kx * cos(w t)` ...(1)

Let first find, value of K, x, w, t

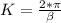`K= (2*\pi)/(\beta )` ....(2)

where β is wavelength in meters

K is wave number

`K= (2*\pi)/(0.01 )`

`K= 628.31 \ m^(-1)`

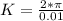
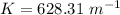
now, let us find value of w

`w = 2 * \pi * f` ....(3)

where f is frequency in hertz

`w = 2 * \pi * 2`

`w = 4 * \pi`

`w= 12.5664 rad`

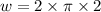
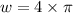
now, let us find value of v that is wave speed

`v= f * \beta`

`v= 2 * 0.04 \\ v= 0.08 (m)/(s)`

`y=(x,t)= 2A * sin Kx * cos(w t)`

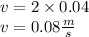
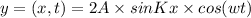
Notice that some x-positions of the resultant wave are always zero no matter what the phase relationship is. These positions are called nodes.

Finding the positions where the sine function equals zero provides the positions of the nodes.

`sin (K * x) = 0 \\ K * x = \pi , 2\pi ,3\pi ,...`

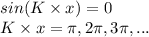
In our case,

`K * x= \pi` and

`x= (\beta )/(2) \\ x= (0.04)/(2) \\x= 0.02`

`y=(0.02,1)= 2A * sin Kx * cos(w t)`

`y=(0.02,1)= 2*0.01 * sin \pi * cos(12.5664 * 1)`

`y=(0.02,1)= 2*0.01 * (-1) * 0.9761`

`y=(0.02,1)= 0.01952 m = 1.952 cm`

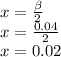
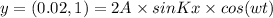
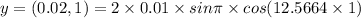
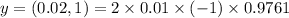
Finally, when bead is at middle of the string, total distance after stretch covered is 1.952 cm.