Question

Approximate to three decimal places using Newton's Method of 3^(-1/4)

and be sure to include the setup with the recursive formula.

Answer 1

• x ≈ 0.760
• f(x) = 3x^4 -1
• 
  `x_(n+1)=(9x^4+1)/(12x^3)`

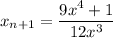
Explanation:

Newton's method seeks a solution to the equation f(x) = 0. The value we seek will be a solution to ...

x = 3^(-1/4)

We can rearrange this to put it into an appropriate form.

x^4 = 3^-1 . . . . . . take 4th powers

3x^4 = 1 . . . . . . . .multiply by 3

3x^4 -1 = 0 . . . . . subtract the right side to make a polynomial in standard form

So, the function we want to find a zero of can be ...

f(x) = 3x^4 -1

The Newton's method iterator for this will be ...

`x_(n+1)=x_n-(f(x_n))/(f'(x_n))\\\\=x_n-(3x^4-1)/(12x^3)=(12x^4-3x^4+1)/(12x^3)\\\\\boxed{x_(n+1)=(9x^4+1)/(12x^3)}`

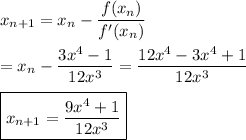
In the attachment, we have defined the iteration function to be g(x). The graph shows us a starting value:
`x_0=0.76`.

Then the first iteration will give accuracy to 3 decimal places*:

x ≈ (9·0.76^4 +1)/(12·0.76^3) = 4.00259584/5.267712 ≈ 0.7598357

The approximate result is x = 0.760.

_____

* The value shown here is actually accurate to 7 decimal places. One more iteration gets accuracy to the full precision of the calculator display.