Question

In triangle JKL, the bisector of angle J divides KL into XK with length y + 3 and XL with length 2y. If JK = 12 and JL = 16, what is the length of XK? *

Answer 1

Answer: so we may be on two differnt triangles since he didnt involve the picture like he shouldve but the answer is 9 in. ill show proof:

Explanation:

Answer 2

The length of XK = 12.7

Explanation:

Given that

JK = 12 , JL = 16 , KX = y + 3 , XL = 2y

From the Δ JKX

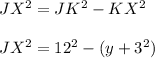`JX^(2) = JK^(2) - KX^(2) \\\\JX^(2) = 12^(2) - (y + 3^(2) )` ----- (1)

From the Δ JXL

`JX^(2) = 16^(2) - (2y)^(2)` ---------- (2)

From Equation (1) & (2) we get

144 - (
`y^(2) + 9 + 6 y) =16 - 4 y^(2)`

`3y^(2) -6y - 121 = 0`

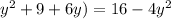
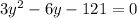
By solving above equation we get

y = 9.7

Therefore the length of XK = y + 3 = 9.7 + 3 = 12.7