Given:
Let time be the independent variable.
Let mile marker be the dependent variable.
On one highway, Gabriela noticed that they passed mile marker 123 at 1:00. She then saw that they reached mile marker 277 at 3:00 and Mr. Morales was driving at a constant speed.
The coordinates of the points on this line are (1,123) and (3,277)
We need to determine the slope of the line.
Slope of the line:
The slope of the line can be determined using the formula,

Substituting the points (1,123) and (3,277) in the above formula, we get;

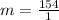
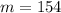
Therefore, the value of the slope of this line is 154.