Answer:
The value of the Discriminant is D=0 in the given quadratic equation .
The value of the discriminant D=0 mean that the number of real number solutions in the equation has double real roots
Explanation:
Given quadratic equation is
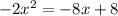
To find : The value of the discriminant .
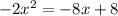
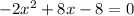
Multiplying by "-" on both sides

Now comparing the above quadratic equation in the standard form of quadratic equation
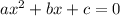 we get.
we get.
The values of , a = 2, b= -8, and c = 8
By Discriminant formula:
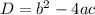
Substituting the values in the formula
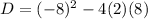
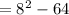
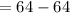

∴ D=0
We know that if the discriminant D= 0, it has double real roots.
∴ The value of the Discriminant is D=0 in the given quadratic equation
The value of the discriminant D=0 mean that the number of real number solutions in the equation has double real roots.