The rate of one cyclist is 9 miles per hour and other cyclist is 18 hours per hour, if the two cyclists start at the same corner and ride in opposite directions. One cyclist rides twice as fast as the other. In 3 hours, they are 81 miles apart.
Explanation:
The given is,
Two cyclists start at the same corner and ride in opposite directions
One cyclist rides twice as fast as the other
In 3 hours, they are 81 miles apart
Step:1
Let, X - Rate of one cyclist
2X - Rate of other cyclist
( One cyclist rides twice as fast as the other )
Step:2
Formula to calculate rate of cyclist,
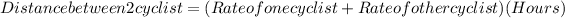
.........................................(1)
From the given values,

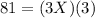
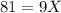
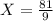
= 9
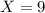
From the X value,
Rate of one cyclist, X = 9 miles per hour
Rate of other cyclist, 2X = 2 × 9
= 18
Rate of other cyclist, 2X = 18 miles per hour
Step:3
Check for solution,
Distance covered by one cyclist = Rate of cyclist × Hours
= 9 × 3 = 27 miles
Distance covered by other cyclist = Rate of cyclist × Hours
= 18 × 3 = 54 miles
From equation (1),
81 = 27 + 54
81 = 81
Result:
The rate of one cyclist is 9 miles per hour and other cyclist is 18 hours per hour, if the two cyclists start at the same corner and ride in opposite directions. One cyclist rides twice as fast as the other. In 3 hours, they are 81 miles apart.