Answer:
Explanation:
If the parabola opens downward, and we have a p value (which is the distance from the vertex to the focus), the form of the equation we need is:

If the vertex is (32, 26), then h = 32 and k = 26. If the focus is located 20 units from the vertex, then p = 20. Filling in:
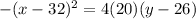 and
and
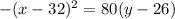 and
and
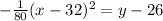 so the equation is
so the equation is

You didn't give choices so I'm not sure what form you need this in. This is vertex (or work) form.