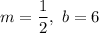Question

Find the slope (m) and the y-intercept (b) of the given line on the graph.

pls show work/explanation!

Answer 1

`\displaystyle y=(1)/(2)x+6`

`\displaystyle m=(1)/(2),\ b=6`

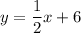
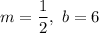
Explanation:

Equation of a Line

Given two points through which a line passes, it's easy to find the equation of the line in the form

`y=mx+b`

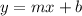
where m is the slope, and b is the y-intercept.

We are given the graph of the line and two clearly marked points to work with: (-4,4) (4,8)

We'll use the point-point formula to build the function of the line

`\displaystyle y-y_1=(y_2-y_1)/(x_2-x_1)(x-x_1)`

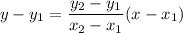
Plugging in the coordinates

`\displaystyle y-4=(8-4)/(4-(-4))(x-(-4))`

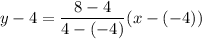
Operating

`\displaystyle y-4=(4)/(8)(x+4)`

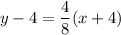
Simplifying

`\displaystyle y-4=(1)/(2)(x+4)`

`\displaystyle y-4=(1)/(2)x+2`

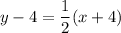
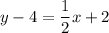
Rearranging

`\displaystyle y=(1)/(2)x+2+4`

`\displaystyle y=(1)/(2)x+6`

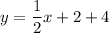
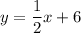
Here we can say

`\displaystyle m=(1)/(2),\ b=6`