1 Answer

Jball · Answer 1 · 2021-03-08T03:15:03+0000

Given:

The given inequality is
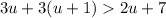
3u+3(u+1)>2u+7

We need to determine the solution of the inequality in interval notation.

Solution of the inequality:

The solution of the inequality can be determined by simplifying the inequality.

Thus, we have,

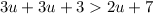
3u+3u+3>2u+7

6u+3>2u+7

Subtracting both sides by 3, we get;

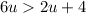
6 u>2 u+4

Subtracting both sides by 2u, we have;

4 u>4

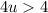
Dividing both sides by 4, we get;

u>1

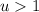
Writing it in interval notation, we get;

$(1, \infty)$

Thus, the solution of the inequality is
$(1, \infty)$

Please log in or register to add a comment.