Question

Someone pleaseee help meee!!!

Answer 1

True

Explanation:

Polar Coordinates

One point in the plane can be expressed as its rectangular coordinates (x,y). Sometimes, it's convenient to express the points in the plane in polar coordinates
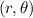`(r,\theta)`, where r is the radius or the distance from the point to the origin, and
`\theta` is the angle measured from the positive x-direction counterclockwise.

The conversion between rectangular and polar coordinates are

`r=√(x^2+y^2)`

`\displaystyle tan\theta=(y)/(x)`

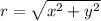
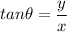
The angle can be computed as the inverse tangent of y/x and it can be negative. It's enough that x and y have opposite signs to make the angle negative. For example, if x=1, y=-1

`\displaystyle tan\theta=(-1)/(1)=-1`

The angle that complies with the above equation is

`\displaystyle \theta=-(\pi)/(4)`

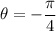
But it can also be expressed as

`\displaystyle \theta=(7\pi)/(4)`

Can the angle be negative? it depends on what is the domain given for
`\theta`. Usually, it's
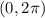`(0,2\pi)` in which case, the angle cannot be negative.

But if the domain was
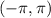`(-\pi,\pi)`, then our first solution is valid and the angle is negative. We'll choose the most general answer: True