Question

A yoga studio sells monthly memberships. The function f(x) = −x2 + 50x − 264 models the profit in dollars, where x is the number of memberships sold.

Determine the zeros, and explain what these values mean in the context of the problem.

x = 6, x = 44; The zeros represent the number of monthly memberships that produces a maximum profit.
x = 6, x = 44; The zeros represent the number of monthly memberships where no profit is made.
x = 25, x = 361; The zeros represent the number of monthly memberships where no profit is made.
x = 25, x = 361; The zeros represent the number of monthly memberships that produces a maximum profit.

Answer 1

Answer: b- x = 6, x = 44; The zeros represent the number of monthly memberships where no profit is made.

Step-by-step explanation: I got it right on the test

Answer 2

x = 6, x = 44; The zeros represent the number of monthly memberships where no profit is made.

Step-by-step explanation:

Here we have the function:

`f(x) = -x^2 + 50x - 264`

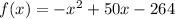
that models the profit in dollars, where x is the number of memberships sold. In order to get the zeros we'll use the quadratic formula:

`\quad x_(1,\:2)=(-b\pm √(b^2-4ac))/(2a) \\ \\ \\ For: \\ \\ a=-1,\:b=50,\:c=-264:\quad x_(1,\:2)=(-50\pm √(50^2-4\left(-1\right)\left(-264\right)))/(2\left(-1\right)) \\ \\ \\ x_(1)=(-50+√(50^2-4\left(-1\right)\left(-264\right)))/(2\left(-1\right))=(-50+√(50^2-4\cdot \:1\cdot \:264))/(-2\cdot \:1)=(-50+√(1444))/(-2\cdot \:1)=6 \\ \\ \\`

`x_(2)=(-50-√(50^2-4\left(-1\right)\left(-264\right)))/(2\left(-1\right))=(-50-√(50^2-4\cdot \:1\cdot \:264))/(-2\cdot \:1)=(-50-√(1444))/(-2)=44`

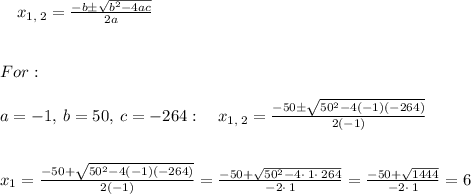
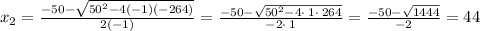
So the zeros are:

`x=6 \\ \\ x=44`

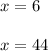
The zeros occurs when
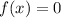`f(x)=0`, so we can conclude that at those points there is no any profit.

In conclusion:

x = 6, x = 44; The zeros represent the number of monthly memberships where no profit is made.