Given:
The given function is
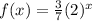
We need to determine the reflection of f(x) over the x - axis
Reflection over x - axis:
The translation rule to reflect over the x - axis is given by
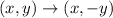
Thus, applying the rule, the function becomes

Multiplying both sides of the equation by -1, we have;
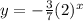
This can be written as
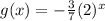
Hence, the reflection of the function over the x - axis is
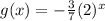
Thus, Option A is the correct answer.