Answer:
The perimeter of the rectangle is 48 m.
Explanation:
Given:
Area of rectangle=153 sq.m
and
width=b and length=l
b=(l-6) m
To find :
Perimeter of given rectangle
Solution:
we know that the
area of rectangle is given by,
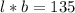
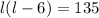
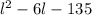 =0
=0
solve this quadratic equation,
we get ,
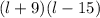
length will not be negative
therefore l=15 m
hence,
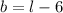
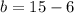
b= 9 m
Now perimeter is
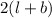
=
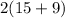
=48 m