Question

Calculus Problem

1. Find the volume of the solid whose base is bounded by the graphs of y = 8 - x^2and y = x^2,
with the indicated cross sections perpendicular to the x-axis:
a. Squares
b. Semi-Circles
C. Equilateral Triangles

Answer 1

The two parabolas intersect for

`8-x^2 = x^2 \implies 2x^2 = 8 \implies x^2 = 4 \implies x=\pm2`

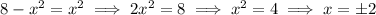
and so the base of each solid is the set

`B = \left\{(x,y) \,:\, -2\le x\le2 \text{ and } x^2 \le y \le 8-x^2\right\}`

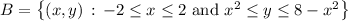
The side length of each cross section that coincides with B is equal to the vertical distance between the two parabolas,
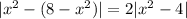`|x^2-(8-x^2)| = 2|x^2-4|`. But since -2 ≤ x ≤ 2, this reduces to
`2(x^2-4)`.

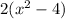a. Square cross sections will contribute a volume of

`\left(2(x^2-4)\right)^2 \, \Delta x = 4(x^2-4)^2 \, \Delta x`

where ∆x is the thickness of the section. Then the volume would be

`\displaystyle \int_(-2)^2 4(x^2-4)^2 \, dx = 8 \int_0^2 (x^2-4)^2 \, dx \\\\ = 8 \int_0^2 (x^4-8x^2+16) \, dx \\\\ = 8 \left(\frac{2^5}5 - \frac{8*2^3}3 + 16*2\right) = \boxed{(2048)/(15)}`

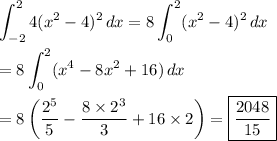
where we take advantage of symmetry in the first line.

b. For a semicircle, the side length we found earlier corresponds to diameter. Each semicircular cross section will contribute a volume of

`\frac\pi8 \left(2(x^2-4)\right)^2 \, \Delta x = \frac\pi2 (x^2-4)^2 \, \Delta x`

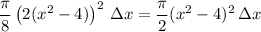
We end up with the same integral as before except for the leading constant:

`\displaystyle \int_(-2)^2 \frac\pi2 (x^2-4)^2 \, dx = \pi \int_0^2 (x^2-4)^2 \, dx`

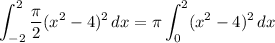
Using the result of part (a), the volume is

`\displaystyle \frac\pi8 * 8 \int_0^2 (x^2-4)^2 \, dx = \boxed{(256\pi)/(15)}}`

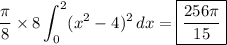
c. An equilateral triangle with side length s has area √3/4 s², hence the volume of a given section is

`\frac{\sqrt3}4 \left(2(x^2-4)\right)^2 \, \Delta x = \sqrt3 (x^2-4)^2 \, \Delta x`

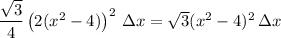
and using the result of part (a) again, the volume is

`\displaystyle \int_(-2)^2 \sqrt 3(x^2-4)^2 \, dx = \frac{\sqrt3}4 * 8 \int_0^2 (x^2-4)^2 \, dx = \boxed{(512)/(5\sqrt3)}`