Question

At 7am you drink a 12-ounce cup of coffee which has 140mg of caffeine. The liver metabolizes caffeine at a rate of 12.9% per hour. How many milligrams of caffeine is in your body after 2 hours? Group of answer choices 136.4 106.2 178.4 33.8

Answer 1

B. 106.2

Explanation:

We have been given that at 7 am you drink a 12-ounce cup of coffee which has 140 mg of caffeine. The liver metabolizes caffeine at a rate of 12.9% per hour. We are asked to find the milligrams of caffeine left in your body after 2 hours.

We will use exponential decay formula to solve our given problem.

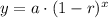`y=a\cdot (1-r)^x`, where,

y = Final value,

a = Initial value,

r = Decay rate in decimal form,

x = Time.

Let us convert 12.9% in decimal form.

`12.9\%=(12.9)/(100)=0.129`

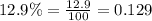
Initial value is 140 mg.

`y=140\cdot (1-0.129)^x`

`y=140\cdot (0.871)^x`

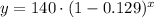
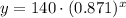
Now we will substitute
`x=2` in our equation as:

`y=140\cdot (0.871)^2`

`y=140\cdot (0.758641)`

`y=106.20974\approx 106.2`

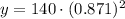
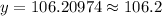
Therefore, approximately 106.2 milligrams of caffeine will be in your body after 2 hours.