Question

Find the volume of a solid generated by revolving the region bounded by the graphs of the equations about the y-axis. Y= 4(3-x), Y= 0, and X= 0.

Answer 1

`\displaystyle V = 36 \pi`

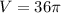
General Formulas and Concepts:

Pre-Algebra

Order of Operations: BPEMDAS

1. Brackets
2. Parenthesis
3. Exponents
4. Multiplication
5. Division
6. Addition
7. Subtraction

• Left to Right

Equality Properties

• Multiplication Property of Equality
• Division Property of Equality
• Addition Property of Equality
• Subtraction Property of Equality

Algebra I

• Graphing
• Coordinates (x, y)
• Functions
• Function Notation
• Intersection Points
• Expand by FOIL

Calculus

Integrals

• Area under the curve

Integration Rule [Reverse Power Rule]:
`\displaystyle \int {x^n} \, dx = (x^(n + 1))/(n + 1) + C`

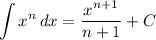
Integration Rule [Fundamental Theorem of Calculus 1]:
`\displaystyle \int\limits^b_a {f(x)} \, dx = F(b) - F(a)`

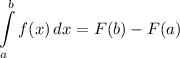
Integration Property [Multiplied Constant]:
`\displaystyle \int {cf(x)} \, dx = c \int {f(x)} \, dx`

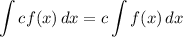
Integration Property [Addition/Subtraction]:
`\displaystyle \int {[f(x) \pm g(x)]} \, dx = \int {f(x)} \, dx \pm \int {g(x)} \, dx`

Volume of Revolution Formula [y-axis]:
`\displaystyle V = \pi \int\limits^b_a {r^2} \, dy`

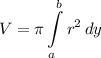
Explanation:

Step 1: Define

Identify

y = 4(3 - x)

y = 0

x = 0

Step 2: Redefine

Rewrite (Revolving around y-axis)

1. [Division Property of Equality] Divide 4 on both sides:
   `\displaystyle (y)/(4) = 3 - x`
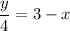
2. [Subtraction Property of Equality] Subtract 3 on both sides:
   `\displaystyle (y)/(4) - 3 = -x`
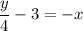
3. [Division Property of Equality] Divide -1 on both sides:
   `\displaystyle 3 - (y)/(4) = x`
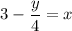
4. Rewrite:
   `\displaystyle x = 3 - (y)/(4)`

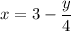
Step 2: Find Bounds of Integration

See attachment

Look at y-values, right to left.

Bounds: [0, 12]

Step 3: Find Volume

1. Substitute in variables [Volume of Revolution Formula]:
   `\displaystyle V = \pi \int\limits^(12)_0 {(3 - (y)/(4))^2} \, dy`
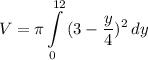
2. [Integrand] Expand [FOIL]:
   `\displaystyle V = \pi \int\limits^(12)_0 {((y^2)/(16) - (3y)/(2) + 9)} \, dy`
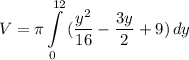
3. [Integral] Rewrite [Integration Property - Addition/Subtraction]:
   `\displaystyle V = \pi \bigg[ \int\limits^(12)_0 {(y^2)/(16)} \, dy - \int\limits^(12)_0 {(3y)/(2)} \, dy + \int\limits^(12)_0 {9} \, dy \bigg]`
4. [Integrals] Rewrite [Integration Property - Multiplied Constant]:
   `\displaystyle V = \pi \bigg[ (1)/(16) \int\limits^(12)_0 {y^2} \, dy - (3)/(2) \int\limits^(12)_0 {y} \, dy + 9 \int\limits^(12)_0 {} \, dy \bigg]`
5. [Integrals] Integrate [Integration Rule - Reverse Power Rule]:
   `\displaystyle V = \pi \bigg[ (1)/(16)((y^3)/(3)) \bigg| \limits^(12)_0 - (3)/(2)((y^2)/(2)) \bigg| \limits^(12)_0 + 9(y) \bigg| \limits^(12)_0 \bigg]`
6. [Integrals] Evaluate [Integration Rule - FTC 1]:
   `\displaystyle V = \pi \bigg[ (1)/(16)(576) - (3)/(2)(72) + 9(12) \bigg]`
7. [Brackets] Multiply:
   `\displaystyle V = \pi [36 - 108 + 108]`
8. [Brackets] Add:
   `\displaystyle V = \pi [36]`
9. Multiply:
   `\displaystyle V = 36 \pi`

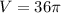
Topic: AP Calculus AB/BC (Calculus I/I + II)

Unit: Applications of Integration

Book: College Calculus 10e