Answer:
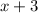 if
if
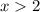
Explanation:
Recall some following basic ideas about absolute value:
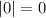 or I guess
or I guess


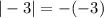 or just
or just
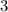 but there is a reason why I wrote it the way I did.
but there is a reason why I wrote it the way I did.
You see that the absolute value returned the same value if the value was positive.
You see that the absolute value returned the opposite value if the value was negative.
You can include 0 in either.
Let's look at
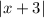 alone for a second.
alone for a second.
*
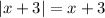 if
if
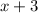 is positive or zero.
is positive or zero.
When is
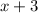 positive or zero? [greater than or equal to 0]
positive or zero? [greater than or equal to 0]
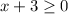
Subtract 3 on both sides

*
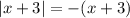 if
if
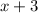 is negative or zero.
is negative or zero.
When is
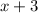 negative or zero? [less or equal to 0]
negative or zero? [less or equal to 0]
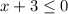
Subtract 3 on both sides
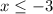
So looking at the bullet points (the *),
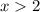 fits into the first inequality.
fits into the first inequality.
Therefore,
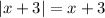 .
.