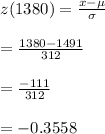Question

A standardized​ exam's scores are normally distributed. In a recent​ year, the mean test score was 1491 and the standard deviation was 312. The test scores of four students selected at random are 1910​, 1230​, 2190​, and 1380. Find the​ z-scores that correspond to each value and determine whether any of the values are unusual.

Answer 1

`z(1910)=1.3429\\\\z(1230)=-0.9006\\\\z(2190)=2.2404\\\\z(1380)=-0.3558`

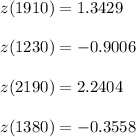
Explanation:

-Given the population mean is
`\mu=1491`and the standard deviation is
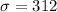`\sigma=312`, we calculate the z-scores using the formula:

`z=(\bar x-\mu)/(\sigma)`

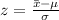
#The z-score for 1910 can be calculated as:

`z(1910)=(x-\mu)/(\sigma)\\\\=(1910-1491)/(312)\\\\=(419)/(312)\\\\=1.3429`

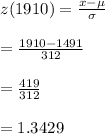
#The z-score for 1230can be calculated as:

`z(1230)=(x-\mu)/(\sigma)\\\\=(1230-1491)/(312)\\\\=(-281)/(312)\\\\=-0.9006`

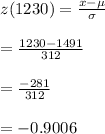
#The z-score for 2190 is calculated as follows:

`z(2190)=(x-\mu)/(\sigma)\\\\=(2190-1491)/(312)\\\\=(699)/(312)\\\\=2.2404`

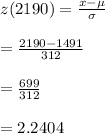
#The z-score for 1380 is calculated as:

`z(1380)=(x-\mu)/(\sigma)\\\\=(1380-1491)/(312)\\\\=(-111)/(312)\\\\=-0.3558`