We'll have to repeatedly square both sides of the equation, in order to get rid of the square roots. Squaring a first time yields
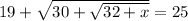
Move the 19 to the right hand side:
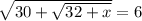
And square again:
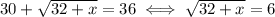
Square one last time:
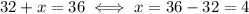
Let's check the solutions: all these squaring might have created external solutions:
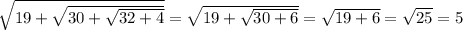
So,
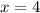 is a feasible solution.
is a feasible solution.